Low-impedance EIS at its Limits: Gamry Reference 30k Booster

Introduction

This Application Note describes measurement of very small impedances using Electrochemical Impedance Spectroscopy (EIS). We recorded EIS spectra of precision current shunts to demonstrate the ability of a Gamry Instruments system to accurately measure impedances less than 100 μΩ. This note discusses the limits in system performance and describes background subtraction to extend performance.
We assume the reader has a basic understanding of EIS and its applications. If you need a refresher, please read Gamry’s Applications Note: “Basics of Electrochemical Impedance Spectroscopy”.

Background

Accurate measurement of low impedance is of greatest importance in electrochemical energy devices (batteries, fuel cells, super-capacitors, photovoltaic cells). Series resistance within these devices causes unwanted power and energy losses.

Sources for series resistance include:

• Contact resistance,
• Resistance of metallic current-collectors,
• Poorly conductive active materials, and
• Resistance in electrolytes and separators. 

Standard practice in electrochemical energy devices sums all series resistive terms into a single term called “Equivalent Series Resistance” or ESR. Batteries, fuel cells, and super-capacitors all require very low ESR to maximize power, energy efficiency and device lifetime.

EIS tests on electrochemical energy devices reveals more than just ESR. EIS can also measure capacitance, electrode porosity, and kinetics of electrochemical reactions. A device’s EIS spectrum typically changes during slow capacity fade and when the device fails. These changes can be used as a diagnostic tool to determine the failure mechanism. Low impedance EIS accuracy is a must for all these measurements.

Low impedance measurements, i.e. below 1 Ω, are most accurately done galvanostatically: an AC current is applied to an electrochemical cell and the AC voltage across the cell is measured. Accurate, very low impedance measurements—below one milliohm (1 mΩ)—are particularly challenging.

These changes can be used as a diagnostic tool to determine the failure mechanism. Accuracy in low-impedance EIS is a must for all these measurements.

Low-impedance measurements, i.e., below 1 Ω, are most accurately done galvanostatically: an AC current is applied to an electrochemical cell and the AC voltage across the cell is measured. Accurate, very low impedance measurements—below 1 mΩ—are particularly challenging. 

For example, assume we want a  1% accurate measurement of a 100 μΩ device using AC stimulation of 1 A_rms. The voltage across the device will be 100 μV_rms so our measurement error must be less than 1 μV_rms. Noise and drift on voltage signals can easily add up to tens of μV, so care and special techniques are needed to resolve one μV.

Higher current makes the voltage bigger so the measurement is easier. Unfortunately higher current often has these limitations:

• Some systems are damaged by high current, 
• High-current, high-power instrumentation can be quite expensive,
• Bandwidth often falls as current increases,
• Cabling can get difficult.  

System and Cable Limitations

Impedances between 1 Ω and 1 kΩ can generally be measured easily and accurately. Details of the test setup and test methodology have little influence on the results. The measured impedance is usually free from artifacts generated by the test system.

As the measured impedance drops the contribution of the measurement system (potentiostat plus cables and connections) becomes a larger factor. There are three ways that most systems limit low impedance measurements:

1)     Instrument noise limits the smallest voltage that can be accurately measured.  EIS uses a phase-sensitive detection scheme to minimize the bandwidth of noise that can affect the measurement, but this can only lower noise, not eliminate it.  Noise in the measured voltage generally causes noise in the reported impedance.   

2)     Real-world instrumentation always has some leakage of the applied signal into the measured signal.  Explanation of the causes of the leakage is beyond the scope of this note. When measuring very small impedances, the voltage signal that represents cell current can be 106 times larger than the sensed voltage signal.2) Real-world instrumentation always has some leakage of the applied signal into the measured signal.  Explanation of the causes of the leakage is beyond the scope of this note. When measuring very small impedances, the voltage signal that represents cell current can be 106 times larger than the sensed voltage signal.Signal leakage error often models as a resistance in series with the “true” cell impedance. The apparent resistance value can be negative!

3)    Additionally, the cell current flowing through the cables connecting the instrument to the cell generates a magnetic field that can be picked up in the voltage sensing leads. This effect, called mutual inductance, is a function of frequency. Mutual inductance error is generally insignificant at low frequency and totally dominates the measurement at high frequency. The impedance error from mutual inductance generally models as an apparent inductance in series with the “true” cell impedance.

Moving the cell leads will change mutual inductance errors. The apparent inductance value can be negative.

Experimental Details

All spectra in this note were recorded using Gamry’s EIS300. The Gamry hardware was a Reference 3000 Potentiostat/Galvanostat/ZRA connected to a Reference 30k Booster. Standard cell cabling was used in a 4 terminal arrangement.

The current shunts were Empro Models HA-400-50, FL 2000-50 and FL-3000-50. The latter two shunts required special connections described at the end of this note.

The Li-Ion battery we tested was a Gaia HP-602050 rated for 45 Ah. The super-capacitor we tested was a Maxwell BCAP0650 P270 rated for 650 F. Both tests used an intermediate state-of-charge on the device.

All shunt tests were done with an applied current of 20 A_rms. The battery and super-capacitor spectra used an excitation of 3 A_rms. Shorted lead tests were measured at both 20 A_rms and 3 Arms so as to best compare with the shunt and device spectra.

Shorted Lead

An EIS system’s minimum impedance characteristic can be measured via a shorted lead test. The cell leads are shorted together and a galvanostatic EIS spectrum is recorded. The excitation current is usually the maximum current allowed in the system.

This test can be very tricky for an EIS system capable of measuring very low impedance. The tester must carefully place the cell leads to avoid errors. One often misunderstood problem in shorted lead tests is the finite resistance of even the most conductive metals. The resistance of a cubic block of copper 1 cm on each side is 1.6 μΩ. While this is very small resistance, it is definitely not zero and can be measured using a good EIS system.

Figure 1 shows the cell lead arrangement Gamry uses to record accurate shorted lead spectra. The current carrying leads (red and green leads) are both bolted to a copper block. The voltage sense leads (blue and white leads) are connected to a post with no current flow through it. The resistance of the copper block is not measured when you use this lead arrangement.

Figure 1.  Shorted lead test fixture. Sense leads are connected at top, current leads at bottom.

The sense leads should be twisted together to minimize loop area for magnetic coupling. The sense leads should be kept far away from the current carrying leads. This minimizes mutual inductance errors. Note that the mutual inductance effect is not very reproducible from one set-up to the next.

The arrangement of the cell leads while testing a real device is likely to be different than the arrangement during the shorted lead test. The mutual inductance error will therefore be different.

Shorted Lead Results

Figure 2 is a Bode plot of the shorted lead spectrum we measured using a boosted system and an excitation current of 20 A_rms. The solid line is a least squares fit of these data to a series RL model.

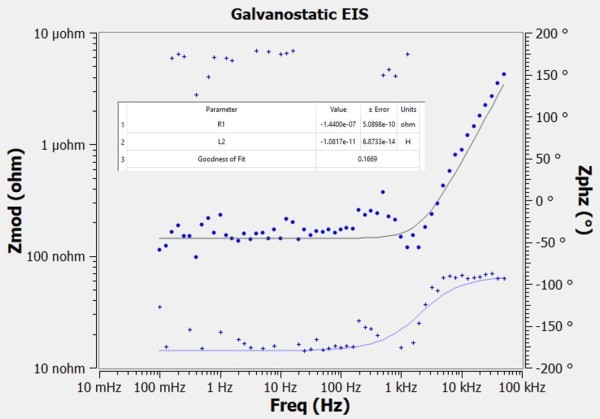
Figure 2 – Shorted-lead spectrum for Reference 3000 with Reference 30k Booster.

The fit values are -144.0 ± 0.5 nΩ and -10.82 ± 0.07 pH. As mentioned above, signal leakage and mutual inductance can cause negative apparent resistance and inductance.

Also note that the phase data looks quite bad. This is simply an artifact of the negative resistance making current and voltage 180° out of phase and noise randomly making that 180° phase either positive or negative.

Surrogate Measurements

In some cases, a cell surrogate gives a better baseline spectrum than the shorted lead experiment described above. A cell surrogate is a very low impedance model of an electrochemical device with the same geometry as the real device. A good example is a fuel cell where a Membrane Electrode Assembly (MEA) is sandwiched between metal plates. The Fuel cell surrogate could use a copper foil in place of the MEA.

In general, a cell surrogate models inductance errors very well since the cell leads can be kept in the same geometry for both the surrogate and the test cell. It is not as good in modeling resistance errors unless the surrogate’s resistance is much smaller than the cell’s resistance.

Cell surrogate measurements were not made on the shunts.

Background Subtraction

Background subtraction is very useful in correcting for low impedance measurement errors. Of course, it is only valid for stable systems.

Gamry’s software allows for subtraction of circuit elements and/or complete spectra. Low impedance errors generally model as impedance in series with a cell under test, so background subtracting a series element or spectrum should always be used for background correction.

We would like to point out two cautions:

1)      The shorted lead spectrum and the surrogate spectrum are each good at modeling one aspect of system behavior but much poorer at modeling other aspects.   Spectrum subtraction can be problematic.  The best correction may be series subtraction of a resistance obtained by modeling a shorted lead spectrum and series subtraction of an inductor obtained from modeling a surrogate spectrum.

2)     Be very careful if the impedance of the system is similar to the background.   Subtraction of two large measured numbers rarely leads to an accurate smaller number.  

Measuring Current Shunts

Current shunts are precision low resistance devices designed for measurement of very high currents. Current shunts are generally designed to produce a 50 mV drop at their rated current level. The shunts used in this note are rated to have error less than 0.25%. They can be purchased for less than US $100.

Impedance Spectra were recorded on shunts with resistance of 16.67 μΩ, 25 μΩ, and 125 μΩ. They were specified for 50 mV drop at 3000 A, 2000 A and 400 A respectively. The shunts are shown in Figure 3.

Figure 3 – . Measured shunts and the shorted-lead test fixture.

125 μΩ Shunt

The first shunt tested was rated for 50 mV at 400 A meaning a resistance of 125.0 ± 0.4 μΩ. This small shunt has a simple setup with only one point of contact on each side for the current connections. Figure 4 shows a Bode plot of this shunt’s impedance spectrum.

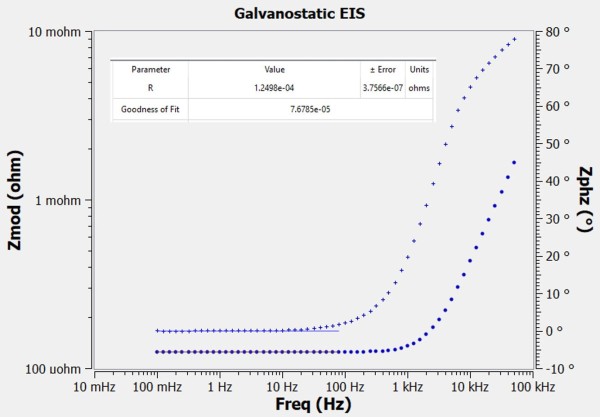
Figure 4 - Impedance spectrum of 125 μΩ shunt

The flat portion of the curve corresponds to 125.0  0.4 μΩ at 0° phase. All measurements up to 100 Hz are flat to within 1% magnitude and within 2° phase.

25 μΩ Shunt

The second shunt tested was rated for 50 mV at 2000 A or 25.00 ± 0.06 μΩ. This shunt (and the one to follow) requires a separate fixture to make proper current connections. The Special Note at the end of this document explains the fixture and physics in more detail. Figure 5 shows a Bode plot of this shunt’s impedance spectrum.

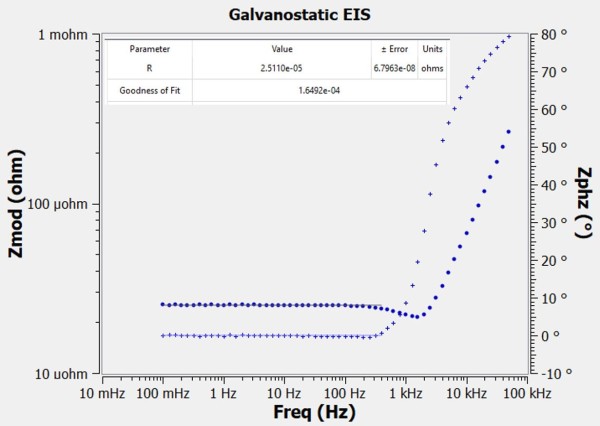
Figure 5 – Impedance spectrum of 25 μΩ shunt

The flat portion of the curve corresponds to 25.11 ± 0.07 μΩ at 0° phase, representing less than 1% deviation from the rated value. All measurements up to 400 Hz are accurate to within 1% magnitude and within 2° phase.

16.67 µΩ Shunt

The third shunt tested was rated for 50 mV at 3000 A, or 16.67 ± 0.04 µΩ. Figure 6 shows a Bode plot of this shunt’s EIS spectrum.




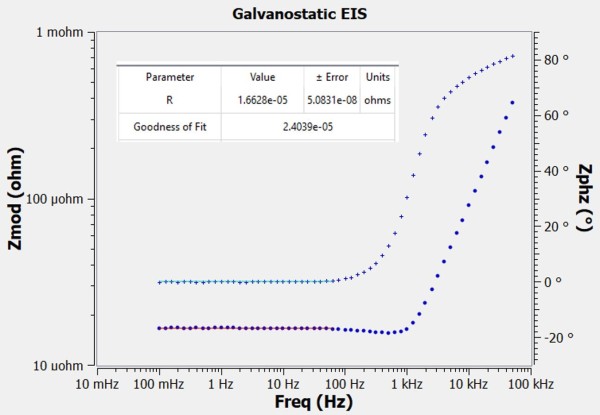
Figure 6 – Impedance spectrum of 16.67 µΩ shunt.

The flat portion of the curve corresponds to 16.63 ± 0.05 μΩ at 0° phase, representing less than 1% deviation from the rated value. All measurements up to 62 Hz are accurate to within 1% magnitude and within 2° phase. Performing a background subtraction of a shorted lead spectrum reduces the magnitude error by a small amount but increases the 1%/2° performance up to 100 Hz.

Shunts and Background

One factor in the EIS300/Reference 3000/Reference 30k Booster system’s impressive performance is its extremely low system background. Figure 7 shows the impedance modulus of the three shunts along with the measured background (shorted lead spectrum) of the same system.


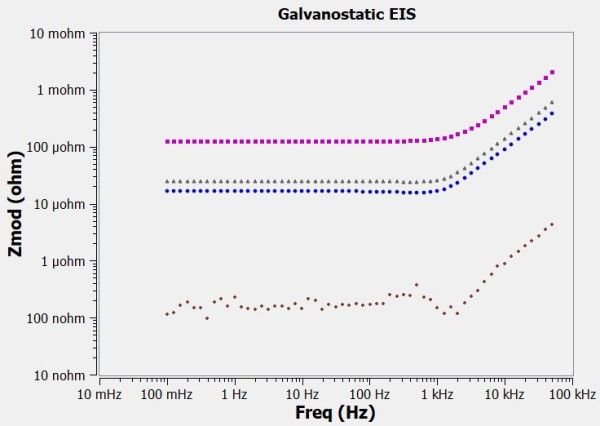
Figure 7 – Impedance modulus of three shunts [125, 25, and 16.67] µΩ and the shorted-lead background.

Measurement of Real Devices

As mentioned in the introduction, very low impedance is of greatest importance in the energy sector. Since ESR directly leads to power loss, minimizing it is critical to device performance. This becomes even more important as the voltage of the device decreases and/or the operating current increases.

Figure 8 shows Nyquist plots of impedance spectra for two current technology devices (a 45 Ah Li-Ion battery and a 650 F super-capacitor) and for the shorted lead spectrum. (Note: this shorted lead spectrum was collected using 3 A_rms AC stimulation).




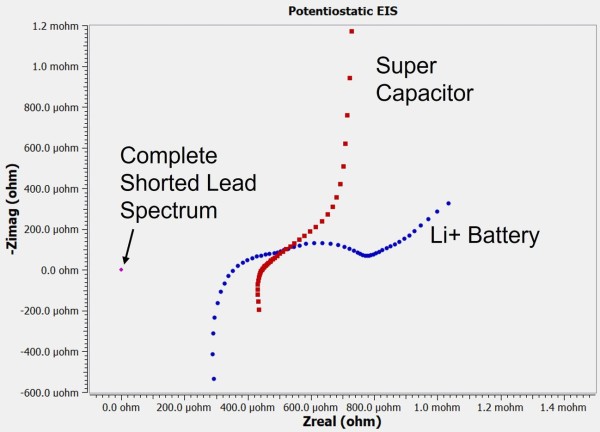
Figure 8 – Nyquist plots for a 650 F super-capacitor, a 45 Ah Li+ battery, and system background.

What looks like a single point at 0-0, is actually the complete shorted lead spectrum over the same frequency range as those of the two devices. Not only do these devices have ESR below 1 mΩ, the impedance over most of their EIS spectra is below 1 mΩ. Next generation devices should exhibit even lower impedance. It is critical to be able to measure these very low impedance levels with confidence.

Two Low-Z Batteries in Parallel

Understanding how to make accurate measurements of shunt resistances has real-world implications. For example, what happens when we connect two very low impedance devices in parallel? The overall Impedance should be reduced as the current now has two low Z pathways to traverse, but in practice, the impedance of the connecting [bus bar] can be larger than the impedance of a single system, making the total system impedance increase, even as the measured impedances of the various processes within the cells decrease.

Figure 9 illustrates the effect for two 302 Ah LiFePO4 (LFP) batteries connected in parallel using one pair of bus bars provided by the vendor. The batteries were tested as received with ESR values of 188 μΩ and 199 μΩ. The impedance of each battery measured separately was reasonably similar. When connected in parallel, the impedance shifts far to the right where the apparent ESR was 1033 μΩ. The true ESR should measure 97 μΩ. Thus, the bus bar pair added 936 μΩ (468 μΩ each bar).

The impedance spectrum in the middle of Figure 9 was measured by adding another pair of bus bars from the vendor, effectively stacking two pairs. As expected, the apparent ESR was reduced to 566 μΩ. Again, the true ESR should measure 97 μΩ. Thus, the stacked bus bars added 469 μΩ, which is half the value measured for a single pair of bus bars. Note that additional bars are in parallel with the first meaning they reduce the added ESR. We can estimate that each bus bar acts as a 469 µΩ resistor in series with the parallel cells. This is consistent with our estimate when only using one bus bar pair.

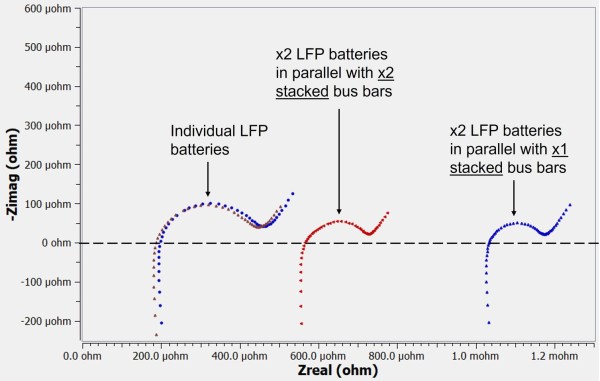
Figure 9- Two LFP batteries connected in parallel

Special Note on Shunt Connections

No matter how good an impedance system is, below 1 mΩ experimental setup becomes critical. Use of twisted pairs and 4-terminal connections is mandatory.

Below 100 μΩ, however, current pathways relative to the sense leads also make a difference. Devices calibrated using a specific geometry (like shunts) make this apparent.

While the higher resistance shunts were designed for a simple 4-probe connection that can be easily made with most potentiostats, the lower impedance shunts needed a special setup to ensure proper current distribution. At these total impedance levels the fractional impedance of the brass block portion of the shunt will affect how current is distributed and impact the measured voltage drop.


Figure 10. Schematic of [16.67, 25] μΩ shunts

This shunt was designed to measure current flowing from the block with the AB pair to the block with the CD pair. The shunt was calibrated with connections utilizing all four bolts.

Ideally, all of the shunt’s resistance will be in the low temperature coefficient metal shown in grey on the diagram. To achieve this, the resistance of the brass blocks must be negligible. We found this is not the case.

We recorded three impedance spectra on the 16.67 μΩ shunt with the current carrying leads:

• Connected to holes A and C,
• Connected to holes B and D, and
• Connected to a fixture that spread the current evenly through the brass blocks. 

Figure 11 shows the resistive portion of the spectra. The data recorded with the even current distribution was close to the nominal value for the shunt. The data with the other connections had errors as large as 4%.

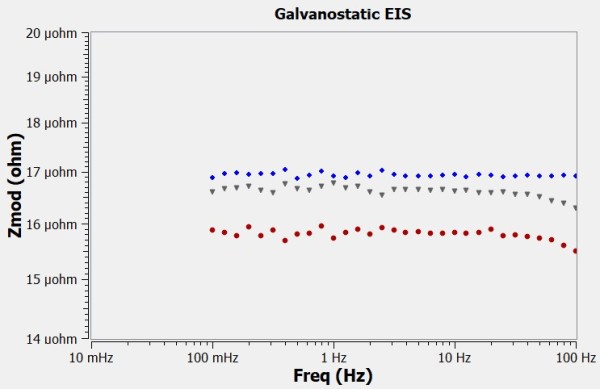
Figure 11 - Blue is A – C, red is B – D, grey is AB – CD

The fixture we used is seen in Figure 12. We used four copper plates to spread the current through the brass blocks.




Figure 12 -  Fixture and setup for appropriate current distribution and accurate 4-terminal measurements on a shunt.

Conclusion

Utilizing an appropriate [cell] setup and using Gamry Instruments’ Reference 3000 with the Reference 30k Booster, accurate EIS measurements of as little as 16.67 μΩ can be made.

Want a PDF version of this application note?

Please complete the following form and we will email a link to your inbox!

First Name:

Surname:

Company Name:

Email address: