Implementation of Transmission Lines Using Generalized Circuit Blocks

Introduction

Transmission lines are regularly used to model the impedance spectra of porous systems. As described in our Transmission Lines application note, distributed elements can be described using these components. Here we will describe the computational aspects of EIS modeling using transmission lines. We assume basic knowledge of transmission lines as covered in our Transmission Lines application note and the information covered in the User Defined Components technical note.

In general, we refer to the circuit blocks that make up the transmission lines as subcomponents. We use χ₁, χ₂, ζ, Z_A and Z_B to denote the subcomponents themselves and their impedances. The symbol “||” indicates a parallel combination.

Three transmission line models shown in Figure 1 are available in Gamry’s Echem Analyst software. These were developed to model diffusion and recombination kinetics by Juan Bisquert. The theory and the applications to dye-sensitized solar cells are explained in a series of papers1.

Figure 1. Three transmission-line equivalent-circuit elements that are available in Echem Analyst.

As we explain later, the “Bisquert Short” (BTS) and the “Bisquert Open” (BTO) components are available for use in either the simplex algorithm or Levenberg-Marquardt algorithm. The “Unified” (UTL) component, on the other hand, is only available for the simplex algorithm because of complications with calculation of the derivative. Therefore we separate our discussion into two parts, first covering BTS and BTO, and second concerning UTL. Each section starts with the mathematical background of the components followed by the software implementation. We then explain the subcomponent calculators. Following this procedure, any transmission line that can be expressed in one of the forms shown in Figure 1 can be defined.

Bisquert Short & Bisquert Open

Mathematical Considerations

The equations to calculate the impedance of the transmission lines are:

(1)

 

where χ = χ({P_i}), ζ = ζ({P_i}), i = 1,2…n and Z = Z({P_i}), i = 0,1,2…n.

For any transmission line, P₀ will always be reserved for L, while P₁,P₂…P_n are parameters of the subcomponents.

To be able to use the transmission lines in Levenberg-Marquardt type fits, we will also need the derivative of Z with respect to each P_i.

∂Z/∂P₀ is straightforward, because there is no L-dependence within χ or ζ:

 

(2)

For i = 1,2,…n, ∂Z/∂P_i have to be calculated using the chain rule. For any given i, you can write the full partial derivative as:

 

You can calculate ∂Z/∂χ and ∂Z/∂ζ directly from Eq. (1):

All that remains is calculation of ∂χ/∂P_i and ∂ζ/∂P_i for substituting into Eq. (3).

Computational Implementation

Equations (1), (2), and (4) are independent of the specific forms of χ and ζ. These are implemented in the functions TransmissionTanhTLS and TransmissionCothTLO in GamryTransmissionLineUtilities and can be used with any subcomponent.

Definitions of the parameters, the components, and the circuit-block calculators are in the project GamryTransmissionLines. This project is put under ..\Extended Components\TransmissionLines2 during the installation.

The calculator functions CBisqTLS and CBisqTLO are simply calls into the utility functions that are described above.

Specific Implementation for χ≡ r_m, ζ ≡ r_k||q_m

By default Bisquert Short and Bisquert Open are defined with χ ≡ r_m, ζ ≡ r_k||q_m. Either component has five parameters (L, r_m, r_k, y_m, and a). The PARAMETER definitions of these are:

static PARAMETER L = {"L","","",false,0.0,true,0.0}; //n=0
static PARAMETER Rm = {"rm","ohm","ohm*cm^2",false,0.0,true,0.0}; //n=1
static PARAMETER Rk = {"rk","ohm","ohm*cm^2",false,0.0,true,0.0}; //n=2
static PARAMETER Ym = {"ym","S*s^a","S*s^a/cm^2",false,0.0,true,0.0}; //n=3
static PARAMETER a = {"a","","",true,1.0,true,0.0}; //n=4

The two component definitions using the above parameter definitions are:

ComponentLib[0]={"BisqTan", 5, CBisqTLS,{&L,&Rm,&Rk,&Ym,&a},IDB_BISQTAN,true};
ComponentLib[1]={"BisqCot", 5, CBisqTLO,{&L,&Rm,&Rk,&Ym,&a},IDB_BISQCOT,true};

The first parameter in the list (P₀) must always be L. The indexing for the rest is P₁=R_m, P₂=R_k, P₃=Y_m, P₄=a. These indices are the positions of these parameters in pParam, and the associated ∂Z/∂P_i, in pdResultdP respectively.

These functions, like the CalcZ functions explained in the “User-defined Components” applications note, have three parts. The first section, labeled “Bookkeeping,” is not strictly necessary, but it makes the code much more readable and tracking of the parameters easier. The second part performs the necessary calculations for the impedance, and the third part calculates the derivatives when necessary.

For a subcomponent with just a resistor, such as χ ≡ r_m defined above, this looks like:

static void chi_res(bool CalculateDerivatives,
                    double const Frequency,
                    double const * const pParam[],
                    COMPLEX * pResult,
                    COMPLEX pdResultdP[])
{
    double Rm = *pParam[1];                   //<Bookkeeping>
    COMPLEX * dResultdRm = &pdResultdP[1];

    pResult->Re = Rm;                        //<Calculation of impedance>
    pResult->Im = 0.0;

    if(!(CalculateDerivatives==0))          //<Calculation of derivatives>
    {
        dResultdRm->Re = 1.0;
        dResultdRm->Im = 0.0;
    }
}

In the <Bookkeeping> part we get the parameter R_m using the pointer that was passed in with the pParam array position 1. This is because R_m was defined as P₁ in the COMPONENT definition. Similarly we use the pointer from pdResultdP array position 1 for the derivative with respect to R_m. The parts <Calculation of impedance> and <Calculation of derivatives> proceed the same way as any user-defined component.

For the subcomponent ζ, the math is somewhat more complicated. ζ has a parallel resistance and constant-phase element combination (i.e., ζ ≡ r_k||q_m),. The impedance is

 

 

 

After expanding and rationalizing:

 

 

 

 

We will leave the derivatives as an exercise to the eager reader. The code then looks like:

static void zeta_cpe_res(bool CalculateDerivatives,
			double const Frequency,
			double const * const pParam[],
			COMPLEX * pResult,
			COMPLEX pdResultdP[])
{
	double Rk = *pParam[2];                                         //<Bookkeeping>
	double Ym = *pParam[3];
	double a = *pParam[4];
	COMPLEX * dResultdRk = &pdResultdP[2];
	COMPLEX * dResultdYm = &pdResultdP[3];
	COMPLEX * dResultda = &pdResultdP[4];

	COMPLEX Complexdenom,divisor;
	double denom;

	double Omega = 2 * PI * Frequency;                            //<Calculation of impedance>
	double term1 = 1.0/Rk + Ym * pow(Omega,a)*cos(a*PI/2.0);
	double term2 = sin(a*PI/2.0)*Yo3*pow(Omega,a);

	denom = pow(term1,2.0)+pow(term2,2.0);

	pResult->Re = term1/denom;
	pResult->Im = -1.0*term2/denom;

	if(!(CalculateDerivatives==0))                               //<Calculation of derivatives>
	{
		Complexdenom.Re = pResult->Re*pResult->Re - pResult->Im*pResult->Im;
		Complexdenom.Im = pResult->Im*pResult->Re + pResult->Re*pResult->Im;
		dResultdRk->Re = complexdenom.Re/(Rk*Rk);
		dResultdRk->Im = complexdenom.Im/(Rk*Rk);

		divisor.Re = -1*pow(Omega,a)*cos(PI*a/2);
		divisor.Im = -1*pow(Omega,a)*sin(PI*a/2);
		dResultdYm.Re=complexdenom.Re*divisor.Re – complexdenom.Im*divisor.Im;
		dResultdYm.Im=complexdenom.Im*divisor.Re + complexdenom.Re*divisor.Im;

		divisor.Re = Ym * log(Omega);
		divisor.Im = Ym * PI/2;
		dResultda.Re = dResultdYm->Re*divisor.Re – dResultdYm->Im*divisor.Im;
		dResultda.Im = dResultdYm->Im*divisor.Re + dResultdYm->Re*divisor.Im;
	}
}

Using these blocks, then, the CalcZ functions CBisqTLS take the form:

static void CBisqTLS(bool CalculateDerivatives,
	               double const Frequency,
	               double const * const pParam[],
	               COMPLEX * const pZ,
	               COMPLEX * const pdZdP[])
{
	TransmissionTanhTLS(CalculateDerivatives,
	Frequency,
	pParam,
	pZ,
	pdZdP,
	*chi_res,                // chi calculator defined above
	*zeta_cpe_res);          // zeta calculator defined above
}

CBisqTLO operates similarly.

Unified (UTL)

As one would expect the equation governing the impedance of “Unified” is much more complex:

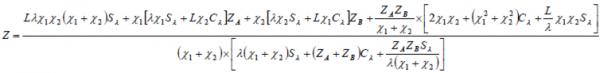
Where C_λ= cosh(L/λ), S_λ = sinh(L/λ) and λ = [ζ/(+)]^1/2.

The major difference between this transmission line and the two before has to do with the calculation of the derivative. The derivatives of this equation would be algebraically and computationally prohibitive to calculate. Therefore, for this type of transmission line, we will only calculate the impedance and not the derivatives. This component can only be used with the simplex method of EIS fitting. To enforce this, LM_Compatible flag is set to false, i.e., no Levenberg-Marquardt fit is allowed.

The component shown above is implemented in GamryTransmissionLineUtilities and named Unified.

The CalcZ type function, CTranLine, is again a straightforward function call. This time, things are even simpler. We do not pass anything related to the derivative calculation.

 

static void CTranLine(bool CalculateDerivatives,
	               double const Frequency,
	               double const * const pParam[],
	               COMPLEX * const pZ,
	               COMPLEX * const pdZdP[])
{
Unified(Frequency,pParam,pZ,*chi1,*zeta,*chi2,*ZACalc,*ZBCalc);
}

pParam holds the pointers to the input parameters and pZ is the pointer to where the calculated impedance goes. These are passed through to the utility function. The last five parameters are the function pointers to the calculators for five subcomponents that are shown in Figure 1c.

As implemented, Unified is defined with χ₁ = r₁, ζ = r₃||q₃, χ₂ =r₂, Z_A = R_A||Q_A and Z_B = R_B. In total, Unified has ten parameters:

static PARAMETER L = {"L","","",false,0.0,true,0.0};                         // n=0
static PARAMETER r1 = {"r1","ohm","ohm*cm^2",false,0.0,true,0.0};            // n=1
static PARAMETER r2 = {"r2","ohm","ohm*cm^2",false,0.0,true,0.0};            // n=2
static PARAMETER r3 = {"r3","ohm","ohm*cm^2",false,0.0,true,0.0};            // n=3
static PARAMETER Yo3 = {"Yo3","S*s^a","S*s^a/cm^2",false,0.0,true,0.0};      // n=4
static PARAMETER a3 = {"a3","","",true,1.0,true,0.0};                        // n=5
static PARAMETER YoA = {"YoA","S*s^a","S*s^a/cm^2",false,0.0,true,0.0};      // n=6
static PARAMETER RA = {"RA","ohm","ohm*cm^2",false,0.0,true,0.0};            // n=7
static PARAMETER aA = {"aA","","",true,1.0,true,0.0};                        // n=8
static PARAMETER RB = {"RB","ohm","ohm*cm^2",false,0.0,true,0.0};            // n=9 

The COMPONENT definition using the above parameter definitions is:

ComponentLib[3] = {"TranLine",10,CTranLine,
                         {&L,&r1,&r2,&r3,&Yo3,&a3,&YoB,&RB,&aB,&RA},IDB_TRANLINE,false};

For the implemented definition, the subcomponent calculators are:

static void chi1_res(double const Frequency,
                        double const * const pParam[],
                        COMPLEX * pResult)
{
	double Resistance = *pParam[1];
	pResult->Re = Resistance;
	pResult->Im = 0.0;
}

static void chi2_res(double const Frequency,
                        double const * const pParam[],
                        COMPLEX * pResult)
{
	double Resistance = *pParam[2];
	pResult->Re = Resistance;
	pResult->Im = 0.0;
}

static void zeta_res_cpe(double const Frequency,
                        double const * const pParam[],
                        COMPLEX * pResult)
{
	double R3 = *pParam[3];
	double Yo3 = *pParam[4];
	double a3 = *pParam[5];
	double Omega = 2 * PI * Frequency;
	double denom;
	double term1 = 1.0/R3 + Yo3 * pow(Omega,a3)*cos(a3*PI/2.0);
	double term2 = sin(a3*PI/2.0)*Yo3*pow(Omega,a3);
	denom = pow(term1,2.0)+pow(term2,2.0);
	pResult->Re = term1/denom;
	pResult->Im = -1.0*term2/denom;
}

static void ZACalc_res_cpe(double const Frequency,
                        double const * const pParam[],
                        COMPLEX * pResult)
{
	double RA = *pParam[7];
	double YoA = *pParam[6];
	double aA = *pParam[8];
	double Omega = 2 * PI * Frequency;
	double denom;
	double term1 = 1.0/RA + YoA * pow(Omega,aA)*cos(aA*PI/2.0);
	double term2 = (sin(aA*PI/2.0)*YoA*pow(Omega,aA));
	denom = pow(term1,2.0)+pow(term2,2.0);
	pResult->Re = term1/denom;
	pResult->Im = -1*term2/denom;
}
static void ZBCalc_res(double const Frequency,
                       double const * const pParam[],
                       COMPLEX * pResult)
{
       double RB = *pParam[9];
       pResult->Re = RB;
       pResult->Im = 0.0;
}

With these five functions above, the CalcZ function CTranline is again very straightforward to implement:

static void CTranLine(bool CalculateDerivatives,
	               double const Frequency,
	               double const * const pParam[],
	               COMPLEX * const pZ,
	               COMPLEX * const pdZdP[])
{
	ASSERT(CalculateDerivatives==False);
	Unified(Frequency,
	      pParam,
	      pZ,
	      *chi1_res,
	      *zeta_res_cpe,
	      *chi2_res,
	      *ZACalc_res_cpe,
	      *ZBCalc_res);
}

Figure 2. A Transmission Line Example to Be Implemented.

 

Defining a New Transmission Line

Now that we have the default components explained, we define a new transmission line. As an example we use a transmission line where the rails are inductors and the steps are capacitors as shown in Figure 2.

Reviewing Figure 2, the first step is to define the parameters and the component itself. We have three parameters: L, l_rail and c_step. The parameter definitions are

 

 

 

static PARAMETER L = {"L","","",false,0.0,true,0.0};
static PARAMETER lrail = {"lrail","H","H/cm^2",false,0.0,true,0.0};
static PARAMETER cstep = {"cstep","F","F/cm^2",false,0.0,true,0.0};

Now that the parameters are defined, we can define our component using these parameters

{"Tutorial”,3,CTutorial,{&L,&lrail,&cstep},IDB_TUTORIAL,true},

The parameter list is—in order—L, lrail, cstep. Therefore we have P₀ = L, P₁ = l_rail, P₂ = c_step. Now we need to implement the functions to calculate the impedances for the rails and the steps. The mathematics is pretty straightforward:

with the derivatives:

The C code for the subcomponent calculators is:

static void chi_ind(bool CalculateDerivatives,
	        double const Frequency,
	        double const * const pParam[],
	        COMPLEX * pResult,
	        COMPLEX pdResultdP[])
{
	double Lrail = *pParam[1];                     //<Bookkeeping>
	COMPLEX * dResultdlrail = &pdResultdP[1];

	double Omega = 2 * PI * Frequency;

	pResult->Re = 0.0;                             //<Calculation of impedance>
	pResult->Im = Omega * lrail;
	if(!(CalculateDerivatives==0))                 //<Calculation of derivatives>
	{
		dResultdlrail->Re = 0.0;
		dResultdlrail->Im = Omega;
	}
}

static void zeta_cap(bool CalculateDerivatives,
	            double const Frequency,
	            double const * const pParam[],
	            COMPLEX * pResult,
	            COMPLEX pdResultdP[])
{
	double Cstep = *pParam[2];                    //<Bookkeeping>
	COMPLEX * dResultdCstep = &pdResultdP[2];

	double Omega = 2 * PI * Frequency;
	double Temp = 1/(Cstep * Omega);

	pResult->Re = 0.0;                           //<Calculation of impedance>
	pResult->Im = -Temp;

	if(!(CalculateDerivatives==0))               //<Calculation of derivatives>
	{
		dResultdlrail->Re = 0.0;
		dResultdlrail->Im = Temp/Cap;
	}
}

With these then the CalcZ function CTutorial reads:

static void CTutorial(bool CalculateDerivatives,
	               double const Frequency,
	               double const * const pParam[],
	               COMPLEX * const pZ,
	               COMPLEX * const pdZdP[])
{
	TransmissionCothTLO(CalculateDerivatives,
		Frequency,
		pParam,
		pZ,
		pdZdP,
		*chi_ind,
		*zeta_cap);
}

Summary

Three separate transmission lines are implemented in the Echem Analyst using generic circuit blocks. As installed, they are implemented with the circuit blocks from Figure 1, and they cover a large subset of what is generally used in the electrochemical literature. There might be cases, however, where a different block would be needed in the transmission line. Fortunately, this only involves changing the calculator for the block and not the entire transmission line. The way our program is implemented, you just need to implement the calculator function for the block and pass it onto the calculator for the transmission line.

Using this procedure, any transmission line that can be expressed in terms of one of three forms in Figure 1 can be implemented and used in the Echem Analyst.

 

---

 1 Bisquert, J. Phys. Chem. Chem. Phys., 2000,2, 4185-4192 ; Bisquert, J. J. Phys. Chem. B 2002, 106, 325-333 ; Fabregat-Santiago, F.; Bisquert, J.; Garcia-Belmonte, G.; Boschloo, G.; Hagfeldt, A. Sol. Ener. Mat. & Sol. Cells 2005,87, 117-131

2 “..\ExtendedComponents” stands for “C:\Documents and Settings\All Users\Application Data\Gamry Instruments\Echem Analyst\Extended Components” in Windows XP and “C:\ProgramData\Gamry Instruments\Echem Analyst\Extended Components” in Windows Vista

Windows is a registered trademark of Microsoft Corporation.

 

Want a PDF version of this application note?

Please complete the following form and we will email a link to your inbox!

First Name:

Surname:

Company Name:

Email address: