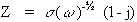
Diffusion can create an impedance known as the Warburg impedance, which depends on the frequency of the potential perturbation. At high frequencies the Warburg impedance is small because diffusing reactants don't have to move very far. At low frequencies the reactants have to diffuse farther, thereby increasing the Warburg impedance.
The equation for the "infinite" Warburg impedance is:
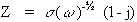
On a Nyquist plot, the infinite Warburg impedance appears as a diagonal line with a slope of 0.5. On a Bode plot, the Warburg impedance exhibits a phase-shift of 45°.
In the previous equation, the Warburg coefficient defined as:
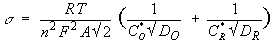
in which
ω = radial frequency (s–1)
DO = diffusion coefficient of the oxidant (cm²/s)
DR = diffusion coefficient of the reductant (cm²/s)
A = surface area of the electrode (cm² )
n = number of electrons transferred
C* = bulk concentration of the diffusing species (moles/cm³ )
The equation for the Warburg impedance can also be written as:
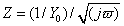
where
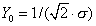
This form of the Warburg impedance is only valid if the diffusion layer has an infinite thickness. Quite often this is not true. If the diffusion layer is bounded, the impedance at lower frequencies no longer obeys the equation above. Instead, we get the form:
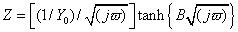
with
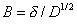
δ = Nernst diffusion layer thickness (cm)
D = an average value of the diffusion coefficients of the diffusing species (cm²/s)
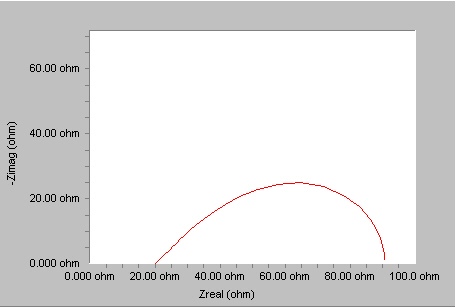
This more general equation is called the Porous Bounded Warburg. You may see this referred to as an "O" circuit element. For high frequencies where ω → ∞, or for an infinite thickness of the diffusion layer where δ → ∞, the previous equation simplifies to the infinite Warburg impedance. A Nyquist plot for a Porous Bounded Warburg is shown below.
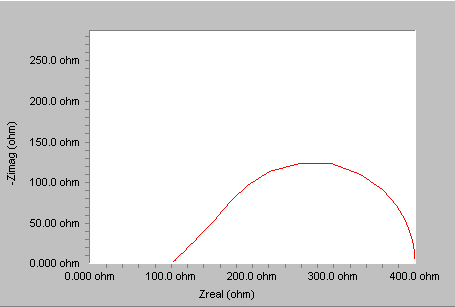
Common examples of a Porous Bounded Warburg are diffusion to a rotated disk electrode or the diffusion of oxygen through a thin coating.
Parameters used for fitting this element are Y0 in siemens•s½, and B in s½.
Another variation of the Warburg is the Bounded Warburg. You may see this referred to as a "T" circuit element.
The Bounded Warburg describes a diffusion process totally within a thin slice of solution or a thin slice of material. Common examples are a conducting polymer membrane or a supercapacitor (an "Electrochemical Capacitor").
For high frequencies where ω → ∞, or for an infinitely thick slice ( where δ → ∞), the previous equation also simplifies to the infinite Warburg impedance, 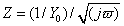 .
.
A sample Nyquist plot is shown below.
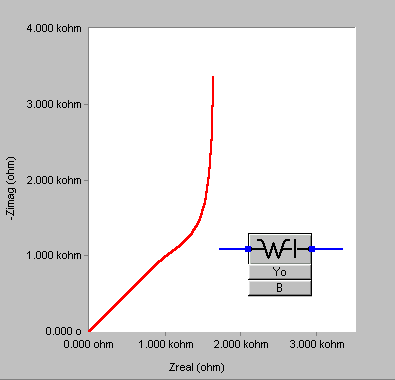
Parameters used for fitting this element are also Y0 in siemens-s½, and B in s½.
One other element is the Gerischer Impedance (G). Its impedance is given by
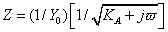
The parameters needed for this element areY0 in siemens•s½, and KA in s–1. A sample plot is shown below.