First consider a cell where semi-infinite diffusion is the rate-determining step, with a series solution resistance as the only other cell impedance.
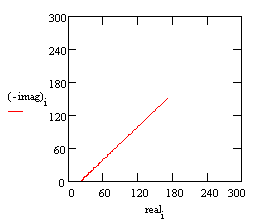
A Nyquist plot for this cell is shown below. Rs was assumed to be 20 Ω. The Warburg coefficient calculated to be about 120 Ω (s)–½ at room temperature for a two-electron transfer, diffusion of a single species with a bulk concentration of 100 mM, and a typical diffusion coefficient of 1.6 ×10–5 cm²/s. Notice that the Warburg impedance appears as a straight line with a slope of 45°.

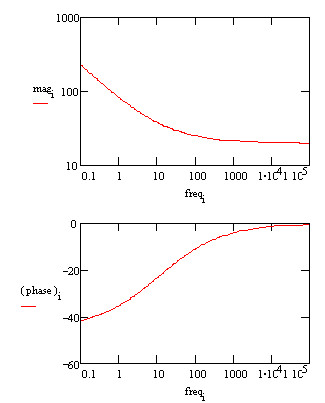
The same data can be plotted in the Bode format. The phase angle of a Warburg impedance is 45°.
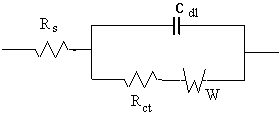
Adding a double-layer capacitance and a charge-transfer impedance, we get the following equivalent circuit.
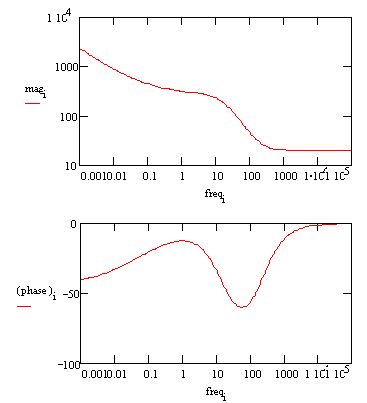
This circuit models a cell where polarization comes from a combination of kinetic and diffusion processes. The Nyquist plot for this circuit is shown below. As in the above example, the Warbug coefficient is assumed to be to be about 150 Ω (s)–½. Other assumptions: Rs = 20 Ω, Rct = 250 Ω, and Cdl = 40 mF.
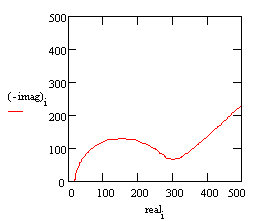
The Bode plot for the same data is also shown below. The lower frequency limit was moved down to 1 mHz to better illustrate the differences in the slope of the magnitude and in the phase between the capacitor and the Warburg impedance. Note that the phase approaches 45° at low frequency.