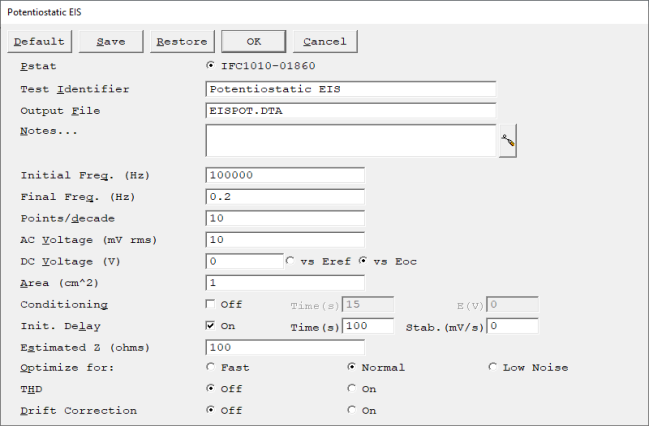
The following parameters are associated with the Potentiostatic EIS experiment.

| Initial Freq. |
The starting point for the frequency sweep during data-acquisition. The frequency is entered in Hertz. The allowed range for Initial Freq. depends upon the potentiostat. Interface 1010T/1010B and Interface 5000P's maximum frequency = 20 kHz Reference 600, Interface 1000E, Interface 3000 and 3000AE, Interface 5000E maximum frequency = 1 MHz Interface 1010E maximum frequency = 2 MHz Reference 600+/620 maximum frequency = 5 MHz |
| Final Freq. |
The ending point for the frequency sweep during data-acquisition. The frequency is entered in Hertz. Interface 1010T/1010B, and Interface 5000P's maximum frequency = 20 kHz Reference 600, Interface 1000E, Interface 3000 and 3000AE, Interface 5000E maximum frequency = 1 MHz Interface 1010E maximum frequency = 2 MHz Reference 600+/620 maximum frequency = 5 MHz EIS scans are usually run with the Initial Freq. larger than the Final Freq. This relationship is not required in the EIS software. NOTE: The frequency sweep may not stop exactly at the final frequency. It is mathematically impossible to control both the Points/decade and Final Freq. parameters exactly for all scan ranges. The EIS software chooses to control the Points/decade parameter exactly. |
| Points/decade |
The density of the data in the impedance spectrum. The data are spaced logarithmically, and the number of data points in each decade in frequency exactly equals Points/decade. As a consequence, the frequency sweep often does not stop exactly at the final frequency. It is guaranteed to do so only when the scan range contains an integer number of decades, such as 5 kHz to 0.05 Hz (5 decades). You can use the Initial Freq., Final Freq., and Points/decade parameters to calculate the total number of data points in the spectrum. Assuming that Initial Freq. = 5000 Final Freq. = 0.2 Points/decade = 10 Then Sweep Range = log (Initial Freq.) – log(Final Freq.) = 3.69 – (–0.69) = 4.39 decades Estimated Points = 1.5 + Sweep Range × Points/decade = 1.5 + 4.39 × 10 = 45.4 Number of Points = 45 points The estimated number of points is always converted to an integer by truncating the fractional part of the number. The spectrum cannot contain more than 32000 data points. This is not a serious limitation, because most impedance spectra contain fewer than 100 points. |
| AC Voltage | The amplitude of the AC signal applied to the cell. The units are rms (root mean square) mV. To convert the entered value into a peak-to-peak value, multiply by √2 (or ~1.414). The resolution of the AC Voltage parameter and its range vary from system to system. They depend on both the FRA and the potentiostat. In general, you can enter values between 1 mV and 1 V. The system does not control the AC Voltage exactly. At higher frequencies, the potentiostat often cannot maintain a one-to-one ratio between the AC signal at the potentiostat input and the resulting signal between the working and reference electrodes. The input signal may need to be 10 or even 100 times larger than the output signal. The EIS software system automatically compensates for this effect. When it does so, it adjusts the applied signal such that the measured AC potential is close to being correct. It does not attempt to keep the measured E signal exactly equal to the AC Voltage parameter. In some cases, the potentiostat simply cannot apply the requested AC voltage. This occurs at high frequency on cells with high solution-resistance. An error message such asUnable to Control AC Cell Voltage should appear on the real-time display. If you see this message, try limiting your sweep range to avoid higher frequencies, lowering the setting on the AC Voltage parameter, or lowering your cell's solution resistance. |
| DC Voltage | The constant potential applied to the cell throughout the frequency sweep. The AC Voltage is summed with the DC Voltage. The DC Voltage is entered in volts. The allowed range is ±8 V with a resolution of 1/8 mV. The voltage can be entered as being absolute (vs. Eref) or relative to the open-circuit potential (vs. Eoc). If the DC Voltage is entered as vs. Eoc, the sum of the measured Eoc and the entered value must be within the range ± 8 V. |
| Estimated Z | An estimate you enter of the cell's impedance at the Initial Freq. It is used to limit the number of trials required before acquiring the first data point in an impedance spectrum. Before taking the first data point, the EIS software sets up the potentiostat and FRA to measure an impedance equal to Estimated Z and tries to measure the cell's impedance. If the estimate is fairly accurate, the first (or second) attempt to measure the impedance will succeed. If the estimate is poor, the system may take up to five trial readings before it finds the correct settings. It is generally sufficient if Estimated Z is within a factor of 5 of the cell's impedance. After the first data point, the last measured impedance is used to calculate new measurement settings, so the entered Estimated Z becomes unimportant. An accurate Estimated Z is more valuable when the initial frequency is low. Note that 1 mHz is 1000 seconds per cycle. Each impedance reading requires at least three cycles at a given frequency, so five readings to find a range at 1 mHz will take over 4 hours! The units for Estimated Z are ohms. There is no reason to enter values larger than 1 TΩ (1012 Ω) or smaller than 0.01 Ω because these values drive the system settings to their most-sensitive and least-sensitive settings, respectively. |
| Optimize for |
A Setup parameter in Electrochemical Impedance Spectroscopy scripts. Optimize for offers three choices: Fast, Normal, and Low Noise.
When you choose Fast, the time required to record a spectrum is much shorter (often by a factor of 5). The fit accuracy is reduced from 99.9% to 99.5%. The maximum number of Lissajous curves is reduced, as low as two at low frequency. The Lissajous curve is not displayed after the first ranging point, so there is no need for delays when the display changes. |
| Drift Correction | Selecting On will enable drift correction during data acquisition. See Common Set-Up Parameters for more information. |
| THD |
Turn on THD to enable Total Harmonic Distortion during the EIS experiment and to obtain the measurement’s harmonic output. |