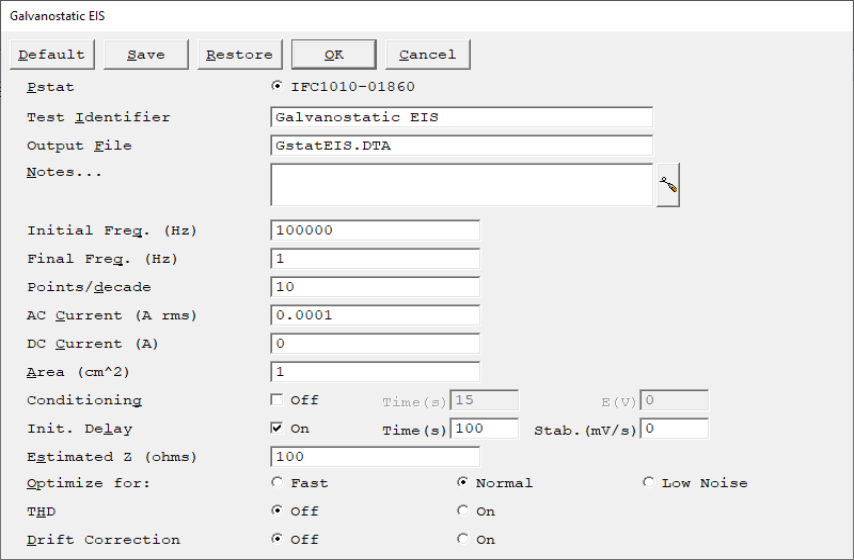
The following parameters are associated with the Galvanostatic EIS experiment.

| Initial Freq. |
The starting point for the frequency sweep during data-acquisition. The frequency is entered in Hertz. The allowed range for Initial Freq. depends upon the potentiostat. Interface 1010T/1010B and Interface 5000P's maximum frequency = 20 kHz Reference 600, Interface 1000E, Interface 3000 and 3000AE, Interface 5000E maximum frequency = 1 MHz Interface 1010E maximum frequency = 2 MHz Reference 600+/620 maximum frequency = 5 MHz |
|
The ending point for the frequency sweep during data-acquisition. The frequency is entered in Hertz. Interface 1010T/1010B, and Interface 5000P's maximum frequency = 20 kHz Reference 600, Interface 1000E, Interface 3000 and 3000AE, Interface 5000E maximum frequency = 1 MHz Interface 1010E maximum frequency = 2 MHz Reference 600+/620 maximum frequency = 5 MHz EIS scans are usually run with the Initial Freq. larger than the Final Freq. This relationship is not required in the EIS software. NOTE: The frequency sweep may not stop exactly at the final frequency. It is mathematically impossible to control both the Points/decade and Final Freq. parameters exactly for all scan ranges. The EIS software chooses to control the Points/decade parameter exactly. |
|
| Points/Decade |
The density of the data in the impedance spectrum. The data are spaced logarithmically, and the number of data points in each decade in frequency exactly equals Points/decade. As a consequence, the frequency sweep often does not stop exactly at the final frequency. It is guaranteed to do so only when the scan range contains an integer number of decades, such as 5 kHz to 0.05 Hz (five decades). You can use the Initial Freq., Final Freq., and Points/decade to calculate the total number of data points in the spectrum. Assuming that Initial Freq. = 5000, Final Freq. = 0.2 and Points/decade = 10 : Sweep Range = log (Initial Freq.) – log(Final Freq.) = 3.69 – (–0.69) = 4.39 decades Estimated Points = 1.5 + Sweep Range × Points/decade = 1.5 + 4.39 × 10 = 45.4 Number of Points = 45 points The estimated number of points is always converted to an integer by truncating the fractional part of the number. The spectrum cannot contain more than 32000 data points. This is not a serious limitation because most impedance spectra contain fewer than 100 points. |
| AC Current |
The amplitude of the AC signal applied to the cell. The units are rms (root mean square) amperes. To convert the entered value into a peak-to-peak value, multiply by 2√2 (or ~2.83). The range of the AC Current parameter is a complex topic. You want an AC Current that keeps the electrochemical cell in a pseudo-linear region of its current-to-voltage curve. In general, avoid AC Currents that create more than 25 mV of rms voltage signal. If your DC Current is zero, the largest AC Current you should enter is about 60% of the instrument's maximum compliance current. You cannot enter the full compliance current, because you are specifying an rms value that is smaller than the peak value. If your DC Current is not zero, you must make sure that the sum of the absolute value of the DC Current and 1.414 times the AC Current does not exceed the instrument's compliance current. If your DC Current is zero, the smallest AC Current that you should enter is a function of the maximum frequency in your experiment. Calculate the ratio of your maximum frequency divided by 100 kHz. Do not enter a current smaller than 5 mA times this ratio. For example, if your maximum frequency is 1 kHz, you can enter a current as small as 50 nA. Regardless of the frequency, we do not recommend entering an AC Current less than 1 nA. If you have a non-zero DC current, we recommend that your AC Current be within two orders of magnitude of the DC Current (between 1% of the DC Current and 100 times the DC Current). The system does not control the AC Current exactly. At higher frequencies, the potentiostat often cannot maintain a one-to-one ratio between the AC signal at the galvanostat input and the resulting current signal. The EIS system automatically compensates for this effect. To do so, it adjusts the applied signal such that the measured AC current is close to being correct. It does not attempt to keep the measured I signal exactly equal to the AC Current parameter. The measured impedance relies on a measured AC Current so this lack of accuracy does to carry over to the experimental results. In some cases, the potentiostat simply cannot apply the requested AC Current. This occurs at high frequency on cells with high solution-resistance. An error message such as Unable to Control AC Cell Current should appear on the real-time display. If you see this message, try limiting your sweep range to avoid higher frequencies, lowering the setting on the AC Current parameter, or lowering your cell's solution resistance. |
| DC Current | The constant current applied to the cell throughout the frequency sweep. The AC Current is summed with the DC Current. In most cases, the DC Current should remain at its default value of zero. The DC Current is entered in amperes. The discussion of AC Current (above) describes some limitations on the DC Current value. |
| Estimated Z |
A user-entered estimate of the cell's impedance at the Initial Frequency. It is used to limit the number of trials required before acquiring the first data point in an impedance spectrum. Before taking the first data point, the EIS software sets up the potentiostat and FRA to measure an impedance equal to Estimated Z and tries to measure the cell's impedance. If the estimate is fairly accurate, the first (or second) attempt to measure the impedance succeeds. If the estimate is poor, the system may take up to five trial readings before it finds the correct settings. It is generally sufficient if Estimated Z is within a factor of 5 of the cell's impedance. After the first data point, the last measured impedance is used to calculate new measurement settings, so the entered Estimated Z becomes unimportant. An accurate Estimated Z is more valuable when the initial frequency is low. Remember, 1 mHz is 1000 seconds per cycle. Each impedance reading requires at least three cycles at a given frequency, so five readings to find a range at 1 mHz will take over 4 hours! The units for Estimated Z are ohms. There is no reason to enter values larger than 1 TΩW (1012Ω or smaller than 0.01 Ω, because these values drive the system settings to their most sensitive and least sensitive settings, respectively. |
| Optimize for |
A Setup parameter in Electrochemical Impedance Spectroscopy scripts. It offers three choices: Fast, Normal, and Low Noise.
The EIS system tries to explain 99.9% of the variation in each Lissajous curve by fitting the E and I data to sine waves at the excitation frequency. It will record and average as many as 20 Lissajous curves to achieve this accuracy. There is a two-second delay after each data point to allow you to examine a Bode plot of the impedance spectrum. With Fast, the time required to record a spectrum is much shorter (often by a factor of 5). The fit accuracy is reduced from 99.9% to 99.5%. The maximum number of Lissajous curves is reduced, as low as 2 at low frequency. The Lissajous curve is not displayed after the first ranging point, so there is no need for delays when the display changes. |
| Drift Correction | Selecting On will enable drift correction during data acquisition. See Common Set-Up Parameters for more information. |
| THD |
Turn on THD to enable Total Harmonic Distortion during the EIS experiment and to obtain the measurement’s harmonic output. |